역전파(Back propagation)
역전파(Back propagation)는 다층 퍼셉트론 모델을 이루는 가중치들을 개선하기 위해 개발된 여러 알고리즘들 중 가장 유명하고 널리 쓰이는 방법입니다.
이번 실습에서는 역전파를 간단하게 실습해보기 위해, 퍼셉트론 한 개의 가중치들을 개선시키는 역전파를 구현해 보도록 합니다.
다음 그림은 이번 실습에서 사용되는 퍼셉트론을 나타냅니다. 입력은 x_1, x_2, x_3 세 개의 정수로 주어지고, 각각 w_1, w_2, w_3의 계수가 곱해져 sigmoid 함수를 통과할 값은 x_1w_1 + x_2w_2 + x_3w_3가 됩니다.
여기서 w_1, w_2, w_3가 바로 우리가 이번 실습에서 알아내야 하는 가중치입니다.
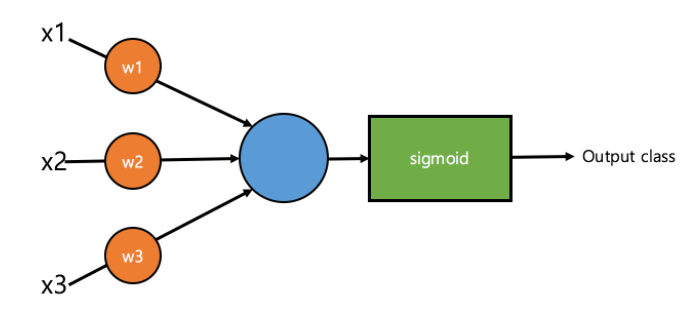
가 sigmoid 함수를 거치고 나면 0 ~ 1 사이의 값으로 변환됩니다. 이는 특정 클래스로 분류될 확률을 나타내며, 0.5보다 작을 경우 0으로, 0.5보다 클 경우 1로 분류된다고 합시다.
이제 이 퍼셉트론을 학습시키려고 합니다. 좀 더 정확히 이야기하면, x_1, x_2, x_3와 그 클래스 y가 여러 개 주어질 때, y값을 가장 잘 예측하는 w_1, w_2, w_3를 찾아야 합니다.
예를 들어, 우리가 갖고 있는 훈련용 데이터가 다음과 같이 3개로 주어진다고 합시다.
- (1, 0, 0) –> 0
- (1, 0, 1) –> 1
- (0, 0, 1) –> 1
그렇다면 w_1 = 0, w_2 = 0, w_3 = 1 이어야 함을 알 수 있습니다.
물론 이와 같은 최적의 w_1, w_2, w_3 값을 처음부터 알 수는 없습니다. 따라서 우선 가중치 w들을 초기화하고, 이를 여러 번의 학습을 거쳐 알아내야 합니다.
즉, 손실 함수(loss function)의 gradient 값을 역전파해서 받은 후, 그 값을 참고하여 손실 함수값을 최소화 하는 방향으로 w_1, w_2, w_3를 업데이트 합니다.
이때, w_1, w_2, w_3이 잘 개선되서 더 업데이트해도 변화가 거의 없을 때까지 하는 것이 중요합니다.
import math
def sigmoid(x) :
return 1 / (1 + math.exp(-x))
'''
X, y 를 가장 잘 설명하는 parameter (w1, w2, w3)를 반환하는
함수를 작성하세요. 여기서 X는 (x1, x2, x3) 의 list이며, y 는
0 혹은 1로 이루어진 list입니다. 예를 들어, X, y는 다음의 값을
가질 수 있습니다.
X = [(1, 0, 0), (1, 0, 1), (0, 0, 1)]
y = [0, 1, 1]
'''
'''
1. 지시 사항을 따라서 getParameters 함수를 완성하세요.
Step01. X의 한 원소가 3개이므로 가중치도 3개가 있어야 합니다.
초기 가중치 w를 [1,1,1]로 정의하는 코드를 작성하세요.
단순히 f = 3, w = [1,1,1]이라고 하는 것보다 좀 더
좋은 표현을 생각해보세요.
Step02. 초기 가중치 w를 모델에 맞게 계속 업데이트 해야합니다.
업데이트를 위해 초기 가중치 w에 더해지는 값들의 리스트
wPrime을 [0,0,0]로 정의하는 코드를 작성하세요.
마찬가지로 단순히 wPrime = [0,0,0]이라고 하는 것보다
좀 더 좋은 표현을 생각해보세요.
Step03. sigmoid 함수를 통과할 r값을 정의해야합니다. r은
X의 각 값과 그에 해당하는 가중치 w의 곱의 합입니다.
즉, r = X_0_0 * w_0 + X_1_0 * w_0 + ... + X_2_2 * w_2
가 됩니다.
그리고 sigmoid 함수를 통과한 r값을 v로 정의합시다.
Step04. 가중치 w가 더이상 업데이트가 안될 때까지 업데이트 해줘야합니다.
즉, 가중치 w의 업데이트를 위해 더해지는 wPrime의 절댓값이 어느 정도까지
작아지면 업데이트를 끝내야 합니다.
그 값을 0.001로 정하고, wPrime이 그 값을 넘지 못하면 가중치
업데이트를 끝내도록 합시다.
다만 wPrime의 절댓값이 0.001보다 작아지기 전까지는 w에 wPrime을 계속
더하면서 w를 업데이트 합시다.
'''
def getParameters(X, y) :
# Step01.
f = len(X[0])
w = [1] * f
values = []
while True :
# Step02.
wPrime = [0] * f
vv = [] # sigmoid를 통과한 r이 들어갈 빈 리스트
# Step03.
for i in range(len(y)) :
r = 0
for j in range(f) :
r = r + X[i][j] * w[j]
v = sigmoid(r)
vv.append(v)
# w를 업데이트하기 위한 wPrime을 역전파를 이용해 구하는 식
for j in range(f) :
wPrime[j] += -((v - y[i]) * v * (1-v) * X[i][j])
# Step04.
flag = False
for i in range(f) :
if abs(wPrime[i]) >= 0.001 :
flag = True
break
if flag == False :
break
for j in range(f) :
w[j] = w[j] + wPrime[j]
return w
def main():
'''
이 코드는 수정하지 마세요.
'''
X = [(1, 0, 0), (1, 0, 1), (0, 0, 1)]
y = [0, 1, 1]
'''
# 아래의 예제 또한 테스트 해보세요.
X = [(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)]
y = [0, 0, 1, 1, 1, 1, 1, 1]
# 아래의 예제를 perceptron이 100% training할 수 있는지도 확인해봅니다.
X = [(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)]
y = [0, 0, 0, 1, 0, 1, 1, 1]
'''
print(getParameters(X, y))
if __name__ == "__main__":
main()
출처: 앨리스 교육
역전파(Back propagation)
역전파(Back propagation)는 다층 퍼셉트론 모델을 이루는 가중치들을 개선하기 위해 개발된 여러 알고리즘들 중 가장 유명하고 널리 쓰이는 방법입니다.
이번 실습에서는 역전파를 간단하게 실습해보기 위해, 퍼셉트론 한 개의 가중치들을 개선시키는 역전파를 구현해 보도록 합니다.
다음 그림은 이번 실습에서 사용되는 퍼셉트론을 나타냅니다. 입력은 x_1, x_2, x_3 세 개의 정수로 주어지고, 각각 w_1, w_2, w_3의 계수가 곱해져 sigmoid 함수를 통과할 값은 x_1w_1 + x_2w_2 + x_3w_3가 됩니다.
여기서 w_1, w_2, w_3가 바로 우리가 이번 실습에서 알아내야 하는 가중치입니다.

가 sigmoid 함수를 거치고 나면 0 ~ 1 사이의 값으로 변환됩니다. 이는 특정 클래스로 분류될 확률을 나타내며, 0.5보다 작을 경우 0으로, 0.5보다 클 경우 1로 분류된다고 합시다.
이제 이 퍼셉트론을 학습시키려고 합니다. 좀 더 정확히 이야기하면, x_1, x_2, x_3와 그 클래스 y가 여러 개 주어질 때, y값을 가장 잘 예측하는 w_1, w_2, w_3를 찾아야 합니다.
예를 들어, 우리가 갖고 있는 훈련용 데이터가 다음과 같이 3개로 주어진다고 합시다.
- (1, 0, 0) –> 0
- (1, 0, 1) –> 1
- (0, 0, 1) –> 1
그렇다면 w_1 = 0, w_2 = 0, w_3 = 1 이어야 함을 알 수 있습니다.
물론 이와 같은 최적의 w_1, w_2, w_3 값을 처음부터 알 수는 없습니다. 따라서 우선 가중치 w들을 초기화하고, 이를 여러 번의 학습을 거쳐 알아내야 합니다.
즉, 손실 함수(loss function)의 gradient 값을 역전파해서 받은 후, 그 값을 참고하여 손실 함수값을 최소화 하는 방향으로 w_1, w_2, w_3를 업데이트 합니다.
이때, w_1, w_2, w_3이 잘 개선되서 더 업데이트해도 변화가 거의 없을 때까지 하는 것이 중요합니다.
import math
def sigmoid(x) :
return 1 / (1 + math.exp(-x))
'''
X, y 를 가장 잘 설명하는 parameter (w1, w2, w3)를 반환하는
함수를 작성하세요. 여기서 X는 (x1, x2, x3) 의 list이며, y 는
0 혹은 1로 이루어진 list입니다. 예를 들어, X, y는 다음의 값을
가질 수 있습니다.
X = [(1, 0, 0), (1, 0, 1), (0, 0, 1)]
y = [0, 1, 1]
'''
'''
1. 지시 사항을 따라서 getParameters 함수를 완성하세요.
Step01. X의 한 원소가 3개이므로 가중치도 3개가 있어야 합니다.
초기 가중치 w를 [1,1,1]로 정의하는 코드를 작성하세요.
단순히 f = 3, w = [1,1,1]이라고 하는 것보다 좀 더
좋은 표현을 생각해보세요.
Step02. 초기 가중치 w를 모델에 맞게 계속 업데이트 해야합니다.
업데이트를 위해 초기 가중치 w에 더해지는 값들의 리스트
wPrime을 [0,0,0]로 정의하는 코드를 작성하세요.
마찬가지로 단순히 wPrime = [0,0,0]이라고 하는 것보다
좀 더 좋은 표현을 생각해보세요.
Step03. sigmoid 함수를 통과할 r값을 정의해야합니다. r은
X의 각 값과 그에 해당하는 가중치 w의 곱의 합입니다.
즉, r = X_0_0 * w_0 + X_1_0 * w_0 + ... + X_2_2 * w_2
가 됩니다.
그리고 sigmoid 함수를 통과한 r값을 v로 정의합시다.
Step04. 가중치 w가 더이상 업데이트가 안될 때까지 업데이트 해줘야합니다.
즉, 가중치 w의 업데이트를 위해 더해지는 wPrime의 절댓값이 어느 정도까지
작아지면 업데이트를 끝내야 합니다.
그 값을 0.001로 정하고, wPrime이 그 값을 넘지 못하면 가중치
업데이트를 끝내도록 합시다.
다만 wPrime의 절댓값이 0.001보다 작아지기 전까지는 w에 wPrime을 계속
더하면서 w를 업데이트 합시다.
'''
def getParameters(X, y) :
# Step01.
f = len(X[0])
w = [1] * f
values = []
while True :
# Step02.
wPrime = [0] * f
vv = [] # sigmoid를 통과한 r이 들어갈 빈 리스트
# Step03.
for i in range(len(y)) :
r = 0
for j in range(f) :
r = r + X[i][j] * w[j]
v = sigmoid(r)
vv.append(v)
# w를 업데이트하기 위한 wPrime을 역전파를 이용해 구하는 식
for j in range(f) :
wPrime[j] += -((v - y[i]) * v * (1-v) * X[i][j])
# Step04.
flag = False
for i in range(f) :
if abs(wPrime[i]) >= 0.001 :
flag = True
break
if flag == False :
break
for j in range(f) :
w[j] = w[j] + wPrime[j]
return w
def main():
'''
이 코드는 수정하지 마세요.
'''
X = [(1, 0, 0), (1, 0, 1), (0, 0, 1)]
y = [0, 1, 1]
'''
# 아래의 예제 또한 테스트 해보세요.
X = [(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)]
y = [0, 0, 1, 1, 1, 1, 1, 1]
# 아래의 예제를 perceptron이 100% training할 수 있는지도 확인해봅니다.
X = [(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)]
y = [0, 0, 0, 1, 0, 1, 1, 1]
'''
print(getParameters(X, y))
if __name__ == "__main__":
main()
출처: 앨리스 교육
