Gradient descent 알고리즘
Gradient descent 알고리즘은 손실 함수(loss function)의 미분값인 gradient를 이용해 모델에게 맞는 최적의 가중치(weight), 즉 손실 함수의 값을 최소화 하는 가중치를 구할 수 있는 알고리즘이다.
이번 실습에서는 Gradient descent 알고리즘을 직접 구현한 후, 이를 이용해 데이터를 가장 잘 설명하는 선형 회귀 직선의 기울기와 y절편, 즉 선형 회귀 모델에게 맞는 최적의 가중치를 찾아보자.
선형 회귀 직선의 수식은 다음과 같은 1차 함수 형태이며, 우리가 Gradient descent 알고리즘을 사용해 찾을 값, 즉 가중치는 w_0과 w_1
f(x) = w_0+w_1 x
손실 함수 (loss function)
손실 함수(loss function)는 실제값과 모델이 예측한 값 간의 차이를 계산해주는 함수로 손실 함수의 값은 가중치와 편향을 업데이트하는 데에 사용된다. 여기서는 손실 함수로 MSE (Mean Squared Error)를 사용하고
MSE는 평균 제곱 오차 함수로, 수식은 다음과 같다.
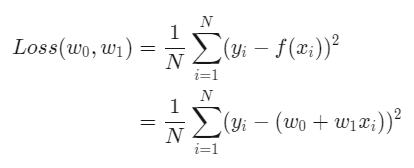
여기서 y_i는 실제값, f(x_i) = w_0+w_1 x_i는 모델 f(x)에 x_i를 넣어서 나온 예측값이다.
편미분
gradient에는 편미분이라는 개념이 들어간다. 때문에 gradient를 설명하기 전 편미분에 대해 간단하게 짚고 넘어가보면! 편미분이란 2개 이상의 변수를 가진 함수에서 우리가 미분할 하나의 변수를 제외한 나머지 변수들을 상수로 보고, 미분 대상인 그 변수로 미분하는 것이다.
예를 들어 f(x,y) = 2x^2+y라는 수식이 있을 때, x에 대해서만 편미분한다면 f ‘(x,y) = \frac{\partial f(x,y)}{\partial x} = 4x가 되는 것이다.
Gradient
gradient는 곧 기울기 벡터를 의미하며, 선형 함수의 각 파라미터들의 편미분으로 구성된 열벡터로 정의!
강의 자료 9페이지를 보면 학습률(learning rate)을 나타내는 \alpha가 있고, gradient를 나타내는 수식인 \triangledown Loss(W)가 있고 즉 이를 풀어서 쓰면 다음과 같은 열벡터 형태이다.
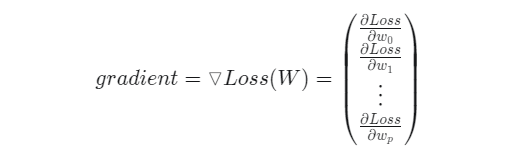
따라서 우리가 구해야 할 w_0와 w_1에 대한 gradient는 다음과 같다.
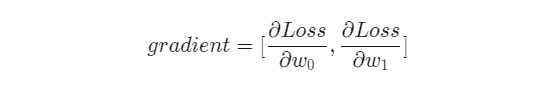
과 w_1에 대한 gradient를 구하기 위해 Loss를 각각에 대해 편미분하면 다음과 같다.
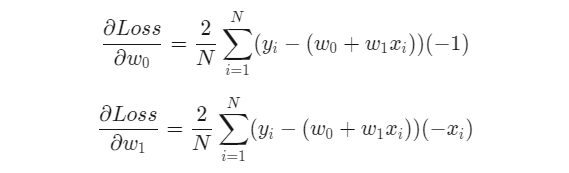
가중치 업데이트
위와 같이 구한 w_0와 w_1의 gradient와 학습률 \alpha를 이용해 가중치를 업데이트하는 공식은 다음과 같다.
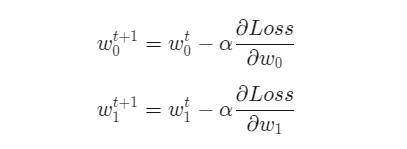
import numpy as np
# 사용할 1차 선형 회귀 모델
def linear_model(w0, w1, X):
f_x = w0 + w1 * X
return f_x
'''
1. 설명 중 '손실 함수' 파트의 수식을 참고해
MSE 손실 함수를 완성하세요.
'''
def Loss(f_x, y):
ls = np.mean(np.square(y - f_x))
return ls
'''
2. 설명 중 'Gradient' 파트의 마지막 두 수식을 참고해 두 가중치
w0와 w1에 대한 gradient인 'gradient0'와 'gradient1'을
반환하는 함수 gradient_descent 함수를 완성하세요.
Step01. w0에 대한 gradient인 'gradient0'를 작성합니다.
Step02. w1에 대한 gradient인 'gradient1'을 작성합니다.
'''
def gradient_descent(w0, w1, X, y):
gradient0 = 2 * np.mean((y - (w0 + w1 * X)) * (-1))
gradient1 = 2 * np.mean((y - (w0 + w1 * X)) * (-1 * X))
return np.array([gradient0, gradient1])
'''
3. 설명 중 '가중치 업데이트' 파트의 두 수식을 참고해
gradient descent를 통한 가중치 업데이트 코드를 작성하세요.
Step01. 앞서 완성한 gradient_descent 함수를 이용해
w0와 w1에 대한 gradient인 'gd'를 정의하세요.
Step02. 변수 'w0'와 'w1'에 두 가중치 w0와 w1을
업데이트하는 코드를 작성합니다. 앞서 정의한
변수 'gd'와 이미 정의된 변수 'lr'을 사용하세요.
'''
def main():
X = np.array([1,2,3,4]).reshape((-1,1))
y = np.array([3.1, 4.9, 7.2, 8.9]).reshape((-1,1))
# 파라미터 초기화
w0 = 0
w1 = 0
# learning rate 설정
lr = 0.001
# 반복 횟수 1000으로 설정
for i in range(1000):
gd = gradient_descent(w0, w1, X, y)
w0 = w0 - lr * gd[0]
w1 = w1 - lr * gd[1]
# 100회마다의 해당 loss와 w0, w1 출력
if (i % 100 == 0):
loss = Loss(linear_model(w0,w1,X),y)
print("{}번째 loss : {}".format(i, loss))
print("{}번째 w0, w1 : {}, {}".format(i, w0, w1),'\n')
return w0, w1
if __name__ == '__main__':
main()
출처: 앨리스 교육
